GRÁFICAS DE LAS FUNCIONES TRIGONOMÉTRICAS

*LINEAS TRIGONOMÉTRICAS

*gráficas de funciones trigonométricas: (gráficas de las funciones seno,coseno,tangente,cotangente,secante y cosecante.)

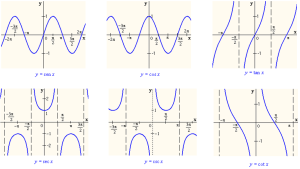
Las gráficas de las funciones trigonométricas  poseen propiedades matemáticas muy interesantes como máximo, mínimo, asíntotas (linea recta que se aproxima continuamente a una función o curva), alcance y periodo entre otras.

Es necesario estudiar la forma de la gráfica de cada función trigonométrica. Esta forma está asociada a las características particulares de cada función.

Al establecer relaciones entre dos conjuntos mediante las funciones trigonométricas se establecen relaciones como y=sen(x), y=cos(x), y=tan(x), y=cot(x), y=csc(x) o y=sec(x). La expresión en el paréntesis se denomina argumento de la función (dominio) mientras que y representa el alcance.

     Las gráficas de estas funciones se extienden sobre los ejes coordenados, si es sobre el eje de x, tienen la característica de repetirse por intervalos. Esto significa que cada cierta cantidad de radianes, una parte de la gráfica de la función es la misma (periodo). La extensión sobre el eje de y se conoce como alcance. Veamos cada función particular en detalle.

 El modelo de las gráficas de las funciones trigonométricas se obtiene evaluando la función para ángulos que forman una revolución completa.

Gráfica de la Función Seno del ángulo

El modelo de la gráfica de la función seno del ángulo se puede obtener transfiriendo puntos del círculo unitario al sistema rectangular de coordenadas. Recuerde que la función seno del ángulo utiliza la y de los arcos del círculo unitario. El ciclo fundamental de la función seno del ángulo comienza en 0 y termina en 2π. En la figura de abajo se observa la relación entre la circunferencia unitaria y la gráfica de la función seno del ángulo x. Esta figura muestra el desarrollo de la gráfica de la funcion seno del angulo x  a partir de la circunferencia unitaria.

Esta función tiene un punto máximo y un punto mínimo en el ciclo fundamental de su gráfica. Veamos las  características de la función Y=(x)

Su dominio es el conjunto de números reales.

Su alcance es el conjunto de números mayores o iguales que menos uno hasta los números menores o iguales que uno.

Su intercepto en el eje de y es el punto (0,0).

El eje de x será el eje de referencia.

El punto máximo del ciclo fundamental tiene coordenadas (π/2,1).

El punto mínimo del ciclo fundamental tiene coordenadas (3π/2,-1).

Su periodo es 2π.

Gráfica de la Función Coseno del ángulo

El modelo de la gráfica de la función coseno del ángulo se puede obtener transfiriendo puntos del círculo unitario al sistema rectangular de coordenadas. Recuerde que la función coseno del ángulo utiliza la x de los arcos del círculo unitario. El ciclo fundamental de la función coseno del ángulo comienza en 0 y termina en 2π. En la figura de abajo se observa la relación entre la circunferencia unitaria y la gráfica de la función coseno del ángulo x. Esta figura muestra el desarrollo de la gráfica de la función del coseno  angulo x  a partir de la circunferencia unitaria.

Esta función tiene un punto máximo y un punto mínimo en el ciclo fundamental de su gráfica. Veamos las características de la función y=cos(x)

Su dominio es el conjunto de números reales

Su alcance es el conjunto de números mayores o iguales que menos uno hasta los números menores o iguales que uno.

Su intercepto en el eje de y es el punto (0,1).

El eje de x será el eje de referencia.

El punto máximo del ciclo fundamental tiene coordenadas (0,1) y (2π,1).

El punto mínimo del ciclo fundamental tiene coordenadas (π,-1).

Su periodo es 2π.

Gráfica de la Función Tangente del ángulo

El modelo de la gráfica de la función tangente del ángulo se puede obtener transfiriendo puntos del círculo unitario al sistema rectangular de coordenadas. Recuerde que la función tangente del ángulo es el cociente de la y y la x de los arcos del círculo unitario. El ciclo fundamental de la función tangente del ángulo comienza en -π/2 y termina en π/2. En la figura de la derecha se observa la relación entre la circunferencia unitaria y la gráfica de la función tangente del ángulo x. Esta figura muestra el desarrollo de la gráfica de la función tangente del angulo x a partir de la circunferencia unitaria.

Esta función tiene asíntotas en el ciclo fundamental de su gráfica. Veamos las características de la gráfica de esta función.

Su dominio es toda x≠π/2±nπ.

Su alcance es el conjunto de todos los números reales.

Su intercepto en el eje de y es el punto (0,0).

El eje de x será el eje de referencia.

Las asíntotas del ciclo fundamental son x=±π/2.

Su periodo es π.

Gráfica de la Función Cotangente del ángulo

El modelo de la gráfica de la función cotangente del ángulo se puede obtener transfiriendo puntos del círculo unitario al sistema rectangular de coordenadas. Recuerde que la función cotangente del ángulo es el cociente de la x y la y de los arcos del círculo unitario. El ciclo fundamental de la función cotangente del ángulo comienza en 0 y termina en π. En la figura de la derecha se observa la relación entre la circunferencia unitaria y la gráfica de la función cotangente del ángulo x.Esta figura muestra el desarrollo de la gráfica de la función cotangente del angulo x  a partir de la circunferencia unitaria.

Esta función tiene asíntotas en el ciclo fundamental de su gráfica. Veamos las características de la gráfica de esta función.

Su dominio es toda x≠±nπ.

Su alcance es el conjunto de todos los números reales.

No tiene intercepto en el eje de y.

El eje de x será el eje de referencia.

Las asíntotas del ciclo fundamental son x=±nπ.

Su periodo es π.

Gráfica de la Función Secante del ángulo

El modelo de la gráfica de la función secante del ángulo se puede obtener transfiriendo puntos del círculo unitario al sistema rectangular de coordenadas o buscando los recíprocos de la función coseno. Recuerde que la función secante del ángulo es el recíproco de la x de los arcos del círculo unitario. El ciclo fundamental de la función secante del ángulo comienza en -π/2 y termina en 3π/2. En la figura de la derecha se observa la relación entre la función coseno y la gráfica de la función secante del ángulo x. Esta figura muestra el desarrollo de la gráfica de la función secante del angulo x a partir de la gráfica de la función coseno del ángulo.

Esta función tiene un punto máximo y un punto mínimo en el ciclo fundamental de su gráfica. También tiene tres asíntotas verticales en su ciclo fundamental. Veamos las características de la gráfica de la función y=sec(x).

Su dominio es el conjunto de números reales excepto los múltiplos impares de π/2.

Su alcance es el conjunto de todos los números menores o iguales que menos uno y todos los números mayores o iguales que uno.

Su intercepto en el eje de y es el punto (0,1).

El eje de x será el eje de referencia.

El punto máximo del ciclo fundamental tiene coordenadas (π,-1).

El punto mínimo del ciclo fundamental tiene coordenadas (0, 1).

Las asíntotas del ciclo fundamental son las ecuaciones x=-π/2, x=π/2 y x=3π/2.

Su periodo es 2π.

Gráfica de la Función Cosecante del ángulo

El modelo de la gráfica de la función cosecante del ángulo se puede obtener transfiriendo puntos del círculo unitario al sistema rectangular de coordenadas o buscando los recíprocos de la función seno. Recuerde que la función cosecante del ángulo es el recíproco de la y de los arcos del círculo unitario. El ciclo fundamental de la función cosecante del ángulo comienza en 0 y termina en 2π. En la figura de la derecha se observa la relación entre la función seno y la gráfica de la función cosecante del ángulo x. Esta figura muestra el desarrollo de la gráfica de la función cosecante del angulo x  a partir de la gráfica de la función seno del ángulo.

 Esta función tiene un punto máximo y un punto mínimo en el ciclo fundamental de su gráfica. También tiene tres asíntotas verticales en su ciclo fundamental. Veamos las características de la gráfica de la función y=csc(x).

Su dominio es el conjunto de números reales excepto los multiplos impares de π/2.

Su alcance es el conjunto de todos los números menores o iguales que menos uno y todos los números mayores o iguales que uno.

Su intercepto en el eje de y es el punto (0,1).

El eje de x será el eje de referencia.

El punto máximo del ciclo fundamental tiene coordenadas (π,-1).

El punto mínimo del ciclo fundamental tiene coordenadas (0, 1).

Las asíntotas del ciclo fundamental son las ecuaciones x=-π/2, x=π/2 y x=3π/2.

Su periodo es 2π.

*ANÁLISIS DE GRÁFICAS (traslación de funciones, reflexión de funciones, comprensión y alargamiento,amplitud,periodo,desfase)

análisis de gráficas:

en la gráfica y análisis de las funciones se estudian sus propiedades, para la cual se utilizan métodos algebraicos y gráficos que incluyen localización de puntos y desplazamientos horizontales y verticales.

traslación de funciones:se puede referir a lo que sigue de f(x) la traslación horizontal es:f(x+c) o f(x-c) y la traslación vertical es:f(x) donde c es una constante.

traslación vertical:

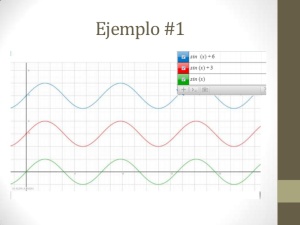
traslación horizontal:

reflexión de funciones:

eje x:

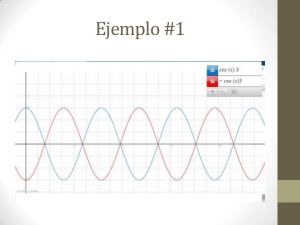
eje y:

comprensión y alargamiento:

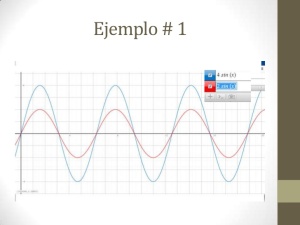
comprensión horizontal:

FUNCIONES TRIGONOMÉTRICAS INVERSAS:las funciones trigonométricas inversas son las funciones inversas de las razones trigonométricas(coseno,seno,tangente)

arcoseno:

el arcoseno es la función inversa del seno, su composición es la identidad, es decir:

Su abreviatura es arcsen o sen-1.

arcocoseno: el arcocoseno es el inverso del coseno,es decir:Al ser el arcocoseno y el coseno funciones inversas, su composición es la identidad, es decir:

Su abreviatura es arccos o cos-1.

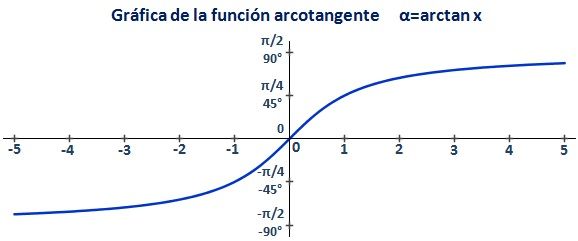
arcotangente: la arcotangente es la función inversa de la tangente, es decir:

Su abreviatura es arctan o tan-1.